64匹马8赛道找前4

• 问题
• 另类解答
• 正统解答

参考这里

问题

64匹马，8个赛道，找出跑得最快的4匹马，至少比赛几场？

另类解答

1. 1场：8个赛道均分为8段，64匹马同时开始
2. 8场：所有马各跑一次，根据用时进行排序

正统解答

1. 全部马分为8组，每组8匹，每组各跑一次，然后淘汰掉每组的后四名，共8场，如下图：

   

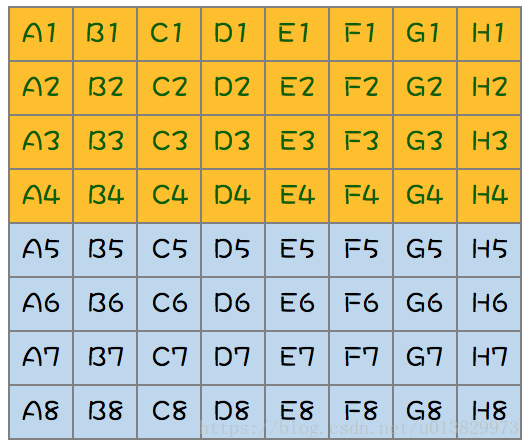
2. 取每组第一名进行一次比赛，然后淘汰最后四名所在组的所有马，共1场，如下图：

   

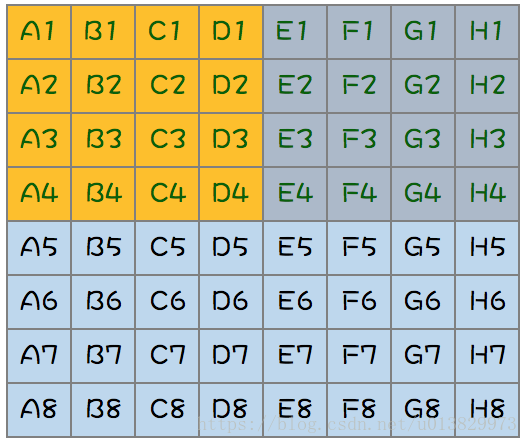
   此时总冠军已经诞生了，它就是A1，蓝色区域（它不需要比赛了）
   而其他可能跑得最快的三匹马只可能是下图中的黄色区域（A2,A3,A4,B1,B2,B3,C1,C2,D1，共9匹马）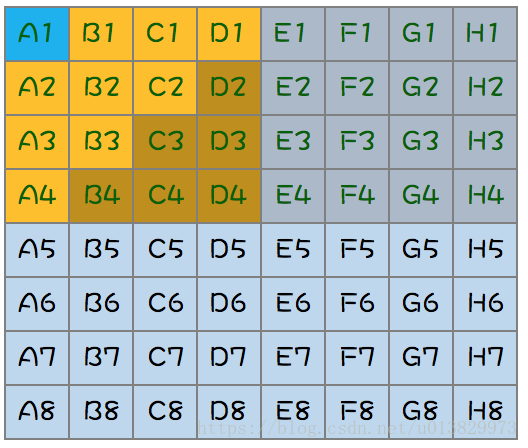

   

3. 从上面的9匹马中找出跑得最快的3匹马

   • 不选A2，剩下8匹马跑一次，如果A3进入前三，则A2入选，踢掉第三
   • 不选B1，剩下8匹马跑一次，如果B2进入前三，则B1入选，踢掉第三
   • 不选C1，剩下8匹马跑一次，如果C2进入前三，则C1入选，踢掉第三

4. 非第三步的三种结果，则需要把第三步的前三和剩余的一匹马再加赛一次，取前三

结论：

1. 顺利情况下：8+1+1=10
2. 不顺利情况下：8+1+1+1=11

至少10场