Algorithm Complexity

• 优劣等级
• 推导步骤
• 推导举例
• 推导简化

在算法分析中，语句总的执行次数T(n)是关于问题规模n的函数。进而分析T(n)随n的变化情况并确定T(n)的数量级，记作：T(n)=O(f(n))，其中f(n)是问题规模n的某个函数。这种用O(f(n))来体现算法时间复杂度的记法，我们称之为大O记法。
一般情况下，随着n的增大，T(n)增长最慢的算法为最优算法。

优劣等级

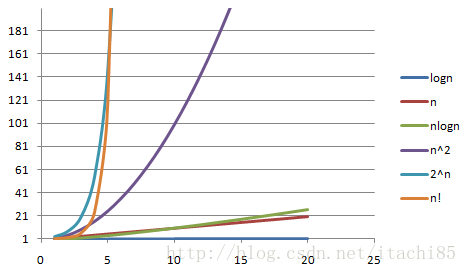
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2 ) < O(n^3 ) < O(2^n ) < O(n!)

即：

常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 立方阶 < 指数阶 < 阶乘阶

下图可以更加直观的展示其复杂度：

ps：如果一个算法是指数阶或者阶乘阶，建议趁早放弃这个算法，去研究新的替代算法吧。因为这两种算法即便是在 n 的规模比较小的情况下仍然要耗费大量的时间，算法的时间复杂度大的离谱，基本上就是“不可用状态”。

推导步骤

1. 计算运行的总次数
2. 用常数1取代运行时间中的所有加法常数
3. 在修改后的运行次数函数中，只保留最髙阶项
4. 如果最高阶项存在且不是1，则去除与这个项相乘的常数

推导举例

1. for循环计算1~100的和

    int sum = 0, n = 100; // 执行1次
    for (int i = 1; i <= n; i++) { // 执行 2*n+2 次
        sum = sum + i; // 执行n次
    }
    System.out.println(sum);// 执行1次
   

   总的执行次数为：3n+4
   根据上述推导步骤，时间复杂度为：O(n)

2. 高斯算法计算1~100的和

    int sum = 0, n = 100; // 执行1次
    sum = (1 + n) * n / 2; // 执行1次
    System.out.println(sum);// 执行1次
   

   总的执行次数为：3
   根据上述推导步骤，时间复杂度为：O(1)

3. 双层for循环

    int n = 100, sum = 0;// 执行1次
    for (int i = 0; i < n; i++) {// 执行2*n+2次
        for (int j = 0; j < n; j++) {// 执行2*n*n+2*n次
            sum++;// 执行n*n次
        }
    }
    System.out.println(sum);// 执行1次
   

   总的执行次数为：3n^2 +4n+4
   根据上述推导步骤，时间复杂度为：O(n^2 )

4. while循环

    int i = 1, n = 100;
    while (i < n) {
        i *= 2;
    }
   

   每次执行i都乘以2，设执行次数为x，那么2x≥n，我们只取等于的情况，得到x=log₂n
   所以时间复杂度为：O(logn)

推导简化

通常不必严格计算算法的运行次数，只需要找到执行次数最多的那条语句（通常是最内层循环的循环体），然后估算其数量级即可（见例4）。